Online
Aktuell 1 Gast und 0 registrierte Benutzer online.
Anmeldung
|
|
| Autor |
Nachricht |
rgerhards
|
|
Titel: Maximale Kosten einer Boole'schen Funktion mit n Variablen
 Verfasst am: 03.10.2008, 12:04 Uhr Verfasst am: 03.10.2008, 12:04 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
| Aufgabenstellung: Zeigen Sie mit Hilfe des Darstellungssatzes, dass die Formelgröße L(f) einer Boole’schen Funktion f(n) in n Variablen weniger als n2^n beträgt. |
|
|
| |
|
|
|
 |
rgerhards
|
|
Titel: Maximale Kosten einer Boole
 Verfasst am: 03.10.2008, 12:05 Uhr Verfasst am: 03.10.2008, 12:05 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
Einige Anmerkungen:
> Es soll bewiesen werden, dass es weniger als n*2^n sind
Wobei mir das vom "Bauchgefühl" her durchaus einleuchtet. Betrachte zum
Beispiel einmal die Kosten der Minterme. Wir gehen ja davon aus, dass jeder
Minterm 2n -1 Kosten verursachen kann. Das stimmt natürlich im schlimmsten
Fall, nämlich dann, wenn alle Variablen invertiert werden müssen. Das kann
aber für eine gegebene n-stellige Schaltfunktion nur genau 1Mal der Fall
sein, nämlich wenn alle Variablen den Wert 0 haben (und dies auch dann nur,
wenn dieser Fall ein Träger der Funktion ist). In allen anderen
Konstellationen müssen aber ein oder mehrere Variablen bereits 1 sein und
müssen daher nicht invertiert werden. Das andere Extrem ist daher, wenn alle
Variablen 1 sind, und auch dieser Fall zum Träger der Funktion gehört. Hier
sind überhaupt keine Invertierungen vorzunehmen, folglich zuählen bei den
Kosten nur noch die Konkunktionen. In diesem bestmöglichen Fall hat der
Minterm dann nur noch Kosten von n-1. Bei allen anderen Fällen Mintermen
liegen die Kosten zwischen den beiden Fällen, also im Interval ]n-1,2n-1[.
Wo sie genau liegen, kann ich allerdings nicht sagen, das kommt eben auf die
Funktion an.
Gleiches für die Anzahl der maximal möglichen Minterme: die sind 2^n, weil
es eben 2^n n-stellige Schaltfunktionen gibt. Der Extremfall ist jetzt hier,
dass die Konstante 1 abgebildet wird. Dann habe ich in der Tat 2^n Minterme
(da ja jede mögliche Kombination die 1 abbildet). Für die Konstante 0, das
andere Extrem, habe ich dagegen genau 0 Minterme, da ja nie die 1 abgebildet
wird. Wenn ich die Extrema ausschliesse, habe ich wieder Werte im
Interval ]1,2^n-1[ an möglichen Mintermen. Die konkrete Anzahl hängt hier
wiederum von der Funktion ab.
Soweit, so gut (na ja...). Ich kann jetzt aber noch etwas folgern, meine ich
zumindest: es besteht ja ein Zusammenhang zwischen den Invertierungen in den
Mintermen und der Anzahl der Minterme. Wenn ich die Wertetabelle einer
n-stelligen Schaltung betrachte, dann merke ich, dass sie maximal
(n2^n)/2-mal Variablen mit Wert 0 beinhalten kann. Lass mich jetzt einfach
mal von dem Extremfall ausgehen, dass die Funktion tatsächlich konstant den
Wert 1 als Ergebnis liefert. Dann habe ich ja tatsächlich 2^n Minterme.
Allerdings kann ich nun auch sicher sagen, dass nicht jeder Minterm die
(maximalen) Kosten von 2n-1 haben kann. Lass' mich das noch einmal
betrachten. Die Kosten der Konjunktionen sind auf jeden Fall da. Also hat
jeder Minterm auf jeden Fall schon einmal Kosten von n-1, die Minterm-Kosten
der Gesamtschaltung somit 2^n*(n-1). Aber Inverter brauche ich wesentlich
weniger, weil ja, salopp gesagt, gar nicht so viel zum invertieren da ist.
Und zwar brauche ich (meiner Meinung nach) nur genau die Hälft der Inverter,
in diesem Extrembeispiel. Im Mittel sind die Kosten für die Inverter ja
Minterm damit nur n/2. Die mittleren Kosten für einen Minterm belaufen sich
damit aber nur noch auf (n-1)+(n/2). Innerhalb der Gesamtschaltung kosten
die Minterme dann 2^n*((n-1)+(n/2)). Mmmhhh... jetzt lass' 'mal rechnen:
2^n*((n-1)+(n/2))
= 2^n*((3n-2)/2)
= 2^n*(1,5n-1)
= 1,5n*2^n-2^n
Das sind aber nur die Kosten für die Minterme. Da fehlen jetzt natürlich
immer noch die Kosten für die Disjunktion der Minterme. Da es 2^n Minterme
gibt, gibt es 2^n-1 Disjunktionen. Die Gesamtkosten der Schaltung betragen
nun
(1,5n*2^n-2^n)+(2^n-1)
oha!
= 1,5n*2^n -2^n+2^n-1
= 1,5n*2^n -1
~ 1,5n*2^n
Das ist natürlich schon etwas erfreulicher, als die Ausgangssituation. Aber
leider ist 1,5n*2^n > n*2^n, nämlich genau 1,5 mal so gross (wenn auch nicht
mehr doppelt). Damit habe ich leider den Beweis nicht erbracht und befinde
mich wiederum in der Sackgasse. Aber geht denn überhaupt weniger, wenn der
Maximalfall abgedeckt werden soll? Ich meine, 1,5n*2^n stellt eine sichere
obere Kostenschranke dar, alles andere müsste billiger sein. Denn dann habe
ich ja entweder weniger Minterme oder weniger Invertierungen. |
|
|
| |
|
|
|
 |
rgerhards
|
|
Titel: Maximale Kosten einer Boole
 Verfasst am: 03.10.2008, 12:21 Uhr Verfasst am: 03.10.2008, 12:21 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
Ein kurzer Gedanke, ehe er verloren geht. Es gibt genau n2^n n-stellige Schaltfunktion. Diese Menge der Möglichen Schaltfunktionen wird partitioniert in die Min- und Maxterme. Man kann eine Schaltung nun aber Realisieren, indem man die kanonische disjunktive Normalform (KDNF) implementiert, also ein boolsches Polynom. Man kann sie aber auch implementieren, indem man die kanonischen konjunktive Normalform (KKNF) implementiert. Diese zeigt alle Fälle, deren Ergebnis 0 ist. Man muss dieses Gesamtergebnis also lediglich invertieren, um zum gleichen Ergebnis zu gelangen wie bei der KDNF.
Damit kann man aber eine Fallunterscheidung treffen. Ist L(KDNF) > L(KKNF), dann wird nicht die KDNF verwendet, sondern die KKFN und deren Ergebnis invertiert. Die Kosten dafür dins L(KKNF) + 1 (für die Invertierung). Unter der Voraussetzung gilt dann im worst case L(KDNF) = L(KKNF)+1, somit ist die Lösung auf jeden Fall die mit den kleinsten Kosten.
Da die Gesamtlösungsmenge in solche mit KKNF und solche mit KDNF partitioniert wird, kann man immer die günstigste von beiden Wählen. Damit sind die Gesamtkosten aber maximal die Hälfte der ansonsten notwendigen Maximalkosten (+1 für die evtl. notwendige Invertierung der KKNF). |
|
|
| |
|
|
|
 |
aschunk
|
|
Titel: Aufgabe 1
 Verfasst am: 03.10.2008, 13:11 Uhr Verfasst am: 03.10.2008, 13:11 Uhr
|
|
Anmeldung: 03. Okt 2008
Beiträge: 313
|
|
Hallo,
so da bin ich. Ich versuche mal zusammen zufassen, was im Skript steht:
Für die Anzahl der Konjunktionen gilt L(f) <= 2n-1, im besten Fall n-1.
Für die Anzahl Minterme #Tr(f) gilt:
#Tr(f) <= #{0,1}^n = 2^n, d.h. die Anzahl der Minterme ist kleiner oder gleich der Anzahl aller Kombinationen der Schaltfunktion also = 2^n.
Für die Anzahl der ODER Kombinationen der Minterme gilt:
v = #Tr(f)-1 wenn #Tr(f) >= 2,
also wenn die Anzahl Minterme größer oder gleich 2 ist oder
= 0 wenn #Tr(f) <= 1, was logisch ist, da man hier nur eine Vollkonjunktion hat und keine ODER Verknüpfung braucht.
Wir haben im schlimmsten Fall mindestens 2n-1 Vollkonjunkionen und n-1 ODER Verknüpfungen und im einfachsten Fall n-1 Vollkonjunktionen und 0 ODER Verknüpfungen.
Im schlimmsten Fall wären es also 3n-1 Kosten? und im besten Fall n-1 Kosten? Für die Vollkonjunktionen? Jetzt komm ich durcheinander... |
|
|
| |
|
|
|
 |
aschunk
|
|
Titel: Nachtrag
 Verfasst am: 03.10.2008, 13:25 Uhr Verfasst am: 03.10.2008, 13:25 Uhr
|
|
Anmeldung: 03. Okt 2008
Beiträge: 313
|
|
Noch ein Nachtrag zur Aufgabe:
Unterscheiden Sie die Fälle #Tr(f) <= 2^n+1 und #Tr(f) >= 2^n+1
Dazu ein Beispiel:
Die zweistellige Funktion ODER mit 2^n = 2 also 2^2 sieht so aus:
A| B | Y
---------
0 0 0
0 1 1
1 0 1
1 1 1
Träger der Funktion - also die Minterme - sind die Fälle (0,1), (1,0), (1,1).
Jetzt die Fallunterscheidung für 2^n-1, also 2^4-1 = 2^2-1 = 2^1 = 2.
Die Anzahl der Minter #Tr(f) ist also <= 2.
Jetzt die Fallunterscheidung für > 2^n-1 = 2^1 = 2.
Die Anzahl der Minterme muss also größer als 2 sein. Für die ODER Funktion trifft nur der letzte Fall zu.
Ein Beispiel für den ersten Fall wäre die Äquivalenz:
A | B | Y
------------
0 0 0
0 1 1
1 0 1
1 1 0
Hier ist die Anzahl der Mintermer kleiner oder gleich 2.
Was mir diese Fallunterscheidung bringen soll, weis ich allerdings auch nicht. |
|
|
| |
|
|
|
 |
aschunk
|
|
Titel: RE: Nachtrag
 Verfasst am: 03.10.2008, 13:26 Uhr Verfasst am: 03.10.2008, 13:26 Uhr
|
|
Anmeldung: 03. Okt 2008
Beiträge: 313
|
|
| Das soll natürlich für 2^n-1 gelten. |
|
|
| |
|
|
|
 |
aschunk
|
|
Titel: RE: Nachtrag
 Verfasst am: 03.10.2008, 13:28 Uhr Verfasst am: 03.10.2008, 13:28 Uhr
|
|
Anmeldung: 03. Okt 2008
Beiträge: 313
|
|
Das Beispiel für die Äquivalenz ist falsch:
A | B | Y
------------
0 0 1
0 1 0
1 0 0
1 1 1
So, aber das Ergebnis ändert sich dadurch nicht. Jetzt hab ich glaub ich erst mal genug geposted. |
|
|
| |
|
|
|
 |
rgerhards
|
|
Titel: RE: Nachtrag
 Verfasst am: 03.10.2008, 16:45 Uhr Verfasst am: 03.10.2008, 16:45 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
Ich werde erst noch einmal ein paar Begrifflichkeiten klären. Damit "eiere" ich gelegentlich noch rum. Das erschwert die Beweisführung unnötig. Melde mich, sobald ich damit durch bin. Und ... danke für den Besuch hier!
Rainer |
|
|
| |
|
|
|
 |
aschunk
|
|
Titel: Minimale Kosten :)
 Verfasst am: 03.10.2008, 17:58 Uhr Verfasst am: 03.10.2008, 17:58 Uhr
|
|
Anmeldung: 03. Okt 2008
Beiträge: 313
|
|
| Eigentlich müsste der Thread ja Minimale Kosten einer Funktion heißen. |
|
|
| |
|
|
|
 |
rgerhards
|
|
Titel: Re: Minimale Kosten :)
 Verfasst am: 03.10.2008, 20:27 Uhr Verfasst am: 03.10.2008, 20:27 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
|
aschunk hat folgendes geschrieben::
Eigentlich müsste der Thread ja Minimale Kosten einer Funktion heißen.
Nein, das sehe ich nicht so  Denn hier geht es nicht darum, die minimalen Kosten ausfindig zu machen. Vielmehr müssen wir suchen, wie wir belegen können, das gewisse Maximalkosten nicht überschritten werden. Es geht also schon um die Maximum, allerdings soll dieses Maximum unterhalb eines gewissen Wertes liegen.... Denn hier geht es nicht darum, die minimalen Kosten ausfindig zu machen. Vielmehr müssen wir suchen, wie wir belegen können, das gewisse Maximalkosten nicht überschritten werden. Es geht also schon um die Maximum, allerdings soll dieses Maximum unterhalb eines gewissen Wertes liegen....
Rainer |
|
|
| |
|
|
|
 |
Oliver
|
|
Titel: Möglicher Lösungsweg
 Verfasst am: 07.10.2008, 04:02 Uhr Verfasst am: 07.10.2008, 04:02 Uhr
|
|
Anmeldung: 07. Okt 2008
Beiträge: 331
|
|
Hallo Beisammen,
@Rainer: Ich gehe mal davon aus, dass Du die Lösung bereits hast, so dass ich Dir hier nicht Neues verrate - ansonsten lies am Besten einfach nicht weiter und überspring diesen Eintrag.
Ich bin überrascht, dass ich immer etwas von "Invertieren" hier und in der Newsgroup lese, denn das ist nach meiner Ansicht nicht notwendig. Der Darstellungssatz sagt, dass ich eine Schaltfunktion sowohl mit Mintermen als auch mit Maxtermen aufbauen kann. (und wie ich das umforme, tut eigentlich nichts zur Sache...)
Wir sind uns vermutlich einig, dass die maximalen Kosten eines Minterms den maximalen Kosten eines Maxterms entsprechen (Maximal benötige ich für einen Term (Min- oder Max-) n-Inverter und n-1 Verknüpfungen.
Also hängen die weiteren Kosten eigentlich nur noch von den Trägern der Schaltfunktion ab. Habe ich (relativ) viele Träger, dann wird z.B. die KDNF recht teuer, dafür die KKNF sehr günstig und auch umgkehrt.
Sei M meine Menge von möglichen Einsetzungen, dann ist #M=2^n. In dieser Menge tummeln sich jetzt meine ganzen Träger der Schaltfunktion. Wenn mehr als die Hälfte der Elemente dieser Menge Träger sind, dann nehme ich doch einfach die billigere Form, die auf den "Nicht"-Trägern basiert (KKNF) und sind mehr als die Hälfte keine Träger der Schaltfunktion, dann wähle ich die KDNF. Sind die beiden Teilmengen (Träger/Nichtträger) gleich groß, dann macht es in Bezug auf die Anzahl der Terme keinen Unterschied, welche Darstellung ich wähle.
Im Worst-Case habe ich also 2^n/2 =2^(n-1) Terme zu berücksichtigen (nämlich genau die Hälfte der möglichen Einsetzungen) und das ist nach meiner Ansicht auch schon das ganze Geheimnis - jetzt nur noch mit den maximalen Kosten eines Terms mutlitiplizieren und berücksichtigen, dass zwischen den Termen auch eine Verknüpfung steht.
Bei Gelegenheit würde mich mal interessieren, was ihr bei Aufgabe 3a geschrieben habt (Das Ding mit dem vollständigen Operatorensystem), 3b ist ja recht unproblematisch. Mir ist bei 3a überhaupt nichts eingefallen und so habe ich einfach mal lustig die Aufgabenstellung umformuliert als Antwort und ein bisschen ausgeschmückt  . Ich lass das auch so stehen, da mich interessiert, ob das noch Punkte geben kann. Was fiel Euch hier ein? . Ich lass das auch so stehen, da mich interessiert, ob das noch Punkte geben kann. Was fiel Euch hier ein?
Oliver |
|
|
| |
|
|
|
 |
rgerhards
|
|
Titel: Re: Möglicher Lösungsweg
 Verfasst am: 07.10.2008, 06:30 Uhr Verfasst am: 07.10.2008, 06:30 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
|
Oliver hat folgendes geschrieben::
@Rainer: Ich gehe mal davon aus, dass Du die Lösung bereits hast, so dass ich Dir hier nicht Neues verrate - ansonsten lies am Besten einfach nicht weiter und überspring diesen Eintrag.
Im Prinzip ja, aber noch nicht formuliert. Daher antworte ich erst später 
Rainer |
|
|
| |
|
|
|
 |
rgerhards
|
|
Titel: Re: Möglicher Lösungsweg
 Verfasst am: 07.10.2008, 07:59 Uhr Verfasst am: 07.10.2008, 07:59 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
So, jetzt habe ich auch getippt. Erst mal meine Lösung (als LaTeX-Quelltext, aber ich denke verständlich - ich hoffe, dass ich hier im Forum noch TeX-Support hinbekomme):
Ich beginne zunächst mit einigen generellen Betrachtungen.
Die Formelgröße $L(f)$ eines Minterms beträgt maximal $2n-1$, da ein Minterm maximal $n$
Invertierungen und maximal $n-1$ $\wedge$-Verknüpfungen benötigt. Die Formelgröße eines Maxterms
beträgt ebenfalls maximal $2n-1$, da ein Maxterm maximal $n$
Invertierungen und maximal $n-1$ $\vee$-Verknüpfungen benötigt.
\emph{Die maximale Formelgröße von Min- und Maxtermen ist also identisch.}
Die Mächtigkeit der Definitionsmenge jeder $n$-stelligen Schaltfunktion beträgt
$2^n$, da es $2^n$ mögliche Belegungen der Eingangsvariablen gibt. Da eine Schaltfunktion
eine Abbildung ist, folgt daraus, das es genau $2^n$ Min- und Maxterme gibt, die
die einzelne Belegung darstellen. Die Zielmenge der hier betrachteten Schaltfunktionen
($f : \{0,1\}^n \rightarrow \{0,1\}$) besteht aus genau den zwei Symbolen 0 und 1.
Die Definitionsmenge kann daher partitioniert werden in solche Urbilder, die
das Bild 0 erzeugen, und solche, die das Bild 1 erzeugen. Die Menge aller
Urbilder, die das Bild 1 erzeugen wird auch \emph{Träger der Funktion}, $Tr(f)$, genannt.
Diese können direkt mittels Mintermen (in der kanonischen disjunktiven Normalform
KDNF) beschrieben werden. Die Menge aller Urbilder,
die das Bild 0 erzeugen kann direkt mittels der Maxterme (in der kanonischen
konjunktiven Normalform KKNF) beschrieben werden.
Sofern eine Schaltfunktion nur mit Mintermen realisiert wird, müssen
maximal $2^n$ Minterme $\vee$-verküpft werden. Daher betragen die maximalen
Kosten aller Minterme $2^n(2n-1)$ und die der $\vee$-Verküpfungen $2^n-1$ (denn
es ist ja immer eine Verknüpfung weniger notwendig). Die Gesamtkosten, bei Realisierung
nur mit Mintermen betragen somit:
$$2^n(2n-1) + (2^n-1)$$
$$= 2^n2n - 2^n + 2^n - 1$$
$$= n2^{n+1} - 1$$
Nach dem Darstellungssatz kann man Schaltfunktionen nun sowohl mit
Mintermen als auch mit Maxtermen realisieren. Beide Realisierungen führen zu
identischen Ergebnissen. \emph{Die maximalen Kosten bei Realisierung mittels
Maxtermen entsprechen}, mit analogem Beweis, \emph{den Kosten der Realisierung mit
Mintermen.}
Aufgrund der Partitionierung der Definitionsmenge ergibt sich ein Zusammenhang
zwischen der Mächtigkeit der Menge der erforderichen Min- und Maxterme:
$$\#\text{Mintermmenge} = \#\text{Defintionsmenge} - \#\text{Maxtermmenge}$$
Daraus lässt sich folgern, dass es immer maximal gleich viel Min- wie Maxterme
gibt, im Regelfall ist die Mächtigkeit einer der beiden Mengen aber geringer.
Da wir die Schaltfunktion aber beliebig sowohl mit Min- als auch Maxtermen
realisieren können, können wir uns für eine beliebige Kombination, und
insbesondere die jeweils billigste, entscheiden. Diese billigste Kombination
erforderert dabei maximal $\frac{\#\text{Definitionsmenge}}{2}$ Min- oder
Maxterme. Da $\#\text{Definitionsmenge} = 2^n$ ist die maximale Anzahl Min-
oder Maxterme somit $\frac{2^n}{2} = 2^{n-1}$.
Hiermit kann man nun die maximalen Kosten einer Schaltfunktion erneut
betrachten. Es müssen also nicht zwingend $2^n$ Minterme miteinander verknüpft
werden, sondern lediglich $2^{n-1}$ Min- oder Maxterme, abhängig davon welche
Menge weniger mächtig ist. Diese Fallunterscheidung will ich in der weiteren
Rechnung nicht berücksichtigen sondern davon ausgegehen, das die Entscheidung
zur Nutzung von Min- oder Maxtermen bereits gefallen ist. Ich bezeichne diese
in Folge nur noch als ``Terme'', damit ist aber immer Minterm oder Maxterm gemeint
und nicht ein beliebiger Term.
Zur Realisierung der Terme benötige ich nach wie vor Kosten von $2n-1$. Die Verküpfung
der Terme untereinander (nun entweder via 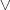 oder oder 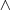 ) hat nun maximal Kosten ) hat nun maximal Kosten
von 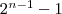 . Die maximalen Gesamtkosten der Schaltfunktion errechnen sich nun . Die maximalen Gesamtkosten der Schaltfunktion errechnen sich nun
wie folgt:
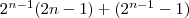
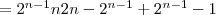
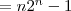
Nun ist aber 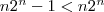 und damit ist der Beweis erbracht, dass sich und damit ist der Beweis erbracht, dass sich
jede beliebige n-stellige Schaltfunktion mit Kosten von weniger als $n2^n$
realisieren lässt. Dabei muss lediglich die geeignete Darstellung als KKNF oder
DKNF gewählt werden. |
Zuletzt bearbeitet von rgerhards am 08.10.2008, 21:03 Uhr, insgesamt ein Mal bearbeitet
|
| |
|
|
|
 |
rgerhards
|
|
Titel: Re: Möglicher Lösungsweg
 Verfasst am: 07.10.2008, 08:29 Uhr Verfasst am: 07.10.2008, 08:29 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
|
Oliver hat folgendes geschrieben::
Ich bin überrascht, dass ich immer etwas von "Invertieren" hier und in der Newsgroup lese, denn das ist nach meiner Ansicht nicht notwendig. Der Darstellungssatz sagt, dass ich eine Schaltfunktion sowohl mit Mintermen als auch mit Maxtermen aufbauen kann. (und wie ich das umforme, tut eigentlich nichts zur Sache...)
Zumindest was mich betrifft, war das mehr Weg als Ziel. Ich habe das gebraucht, um den Darstellungssatz richtig zu verstehen. Wobei ich zuerst schon der Meinung war, ich müsste anschließend invertieren. Aber das hat sich gelegt 
Oliver hat folgendes geschrieben::
Wir sind uns vermutlich einig, dass die maximalen Kosten eines Minterms den maximalen Kosten eines Maxterms entsprechen (Maximal benötige ich für einen Term (Min- oder Max-) n-Inverter und n-1 Verknüpfungen.
ja
Oliver hat folgendes geschrieben::
Also hängen die weiteren Kosten eigentlich nur noch von den Trägern der Schaltfunktion ab. Habe ich (relativ) viele Träger, dann wird z.B. die KDNF recht teuer, dafür die KKNF sehr günstig und auch umgkehrt.
Sei M meine Menge von möglichen Einsetzungen, dann ist #M=2^n. In dieser Menge tummeln sich jetzt meine ganzen Träger der Schaltfunktion. Wenn mehr als die Hälfte der Elemente dieser Menge Träger sind, dann nehme ich doch einfach die billigere Form, die auf den "Nicht"-Trägern basiert (KKNF) und sind mehr als die Hälfte keine Träger der Schaltfunktion, dann wähle ich die KDNF. Sind die beiden Teilmengen (Träger/Nichtträger) gleich groß, dann macht es in Bezug auf die Anzahl der Terme keinen Unterschied, welche Darstellung ich wähle.
Im Worst-Case habe ich also 2^n/2 =2^(n-1) Terme zu berücksichtigen (nämlich genau die Hälfte der möglichen Einsetzungen) und das ist nach meiner Ansicht auch schon das ganze Geheimnis - jetzt nur noch mit den maximalen Kosten eines Terms mutlitiplizieren und berücksichtigen, dass zwischen den Termen auch eine Verknüpfung steht.
Da kann ich Dir mittlerweile zustimmen.
Oliver hat folgendes geschrieben::
Bei Gelegenheit würde mich mal interessieren, was ihr bei Aufgabe 3a geschrieben habt (Das Ding mit dem vollständigen Operatorensystem), 3b ist ja recht unproblematisch. Mir ist bei 3a überhaupt nichts eingefallen und so habe ich einfach mal lustig die Aufgabenstellung umformuliert als Antwort und ein bisschen ausgeschmückt  . Ich lass das auch so stehen, da mich interessiert, ob das noch Punkte geben kann. Was fiel Euch hier ein?
Mein Ansatz ist zu zeigen, dass wenn ich jeden Operator aus O1 durch einen aus O2 ersetzen kann, diese ja offensichtlich funktional äquivalent zueinander sind. Daher sind Aussagen bezüglich der Funktion des jeweiligen Operatorensystems ebenfalls äquivalent. Auch die Vollständigkeits-Aussage ist eine Aussage über das Operatorensystem. Somit gilt sie auch äquivalent. Daher ist O2 ebenfalls vollständig.
Rainer |
|
|
| |
|
|
|
 |
Oliver
|
|
Titel: Re: Möglicher Lösungsweg
 Verfasst am: 07.10.2008, 17:43 Uhr Verfasst am: 07.10.2008, 17:43 Uhr
|
|
Anmeldung: 07. Okt 2008
Beiträge: 331
|
|
Schon mal ein gutes Zeichen, dass wir uns über den Lösungsweg einig sind 
Und für 3b bin ich mal gespannt, ob ich einen Punkt bekomme  |
|
|
| |
|
|
|
 |
|
|
|
|
|
|
|
 ::
::