| Author |
Message |
rgerhards
|
|
Post subject: Bedeutung des Vorzeichenbits in Zweierkomplementdarstellung
 Posted: Dec 11, 2009 - 09:58 AM Posted: Dec 11, 2009 - 09:58 AM
|
|
Joined: Sep 25, 2006
Posts: 688
Status: Offline
|
|
Ich versuche es einmal zu skizzieren: Sei ![[a_{(n-1)}, ..., a_0] [a_{(n-1)}, ..., a_0]](modules/PNphpBB2/latexrender/pictures/0c2fbf94cfb036637524215fcf62d747.png) die n-stellige Zweierkomplementdarstellung einer Ganzzahl. Dann ist die n-stellige Zweierkomplementdarstellung einer Ganzzahl. Dann ist 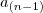 das "Vorzeichenbit". Das Bit kodiert aber nicht nur das Vorzeichen, sondern kann auch als Wert das "Vorzeichenbit". Das Bit kodiert aber nicht nur das Vorzeichen, sondern kann auch als Wert 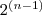 betrachtet werden. Das macht man auch so. Der Wert einer Zahl in Zweierkomplementdarstellung ist dann: betrachtet werden. Das macht man auch so. Der Wert einer Zahl in Zweierkomplementdarstellung ist dann:
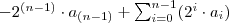
oder, in Prosa: Du bildest die Summe über alle Bits ausser dem höchstwertigen und subtrahierst dann den Wert des höchstwertigen Bits von dieser Summe. Das Ergebnis ist dann der darzustellende Wert.
Nehmen wir nun an, du möchtest die n-stellige Darstellung in eine (n+1)-stellige erweitern. Ist der Wert positiv, so kannst ist der Wert der höchstwertigen Stelle 0 ![[0 * 2^{(n-1)}] [0 * 2^{(n-1)}]](modules/PNphpBB2/latexrender/pictures/687fba47162e4524be670858c9c9a293.png) , der Wert wird somit vollkommen durch das Summenzeichen bestimmt. Du musst also eine 0 an der (n+1)-ten Stelle einfügen. Das ist meist einsichtig, weil es auch unserer gewohnten Schreibweise im Dezimalsystem entspricht. , der Wert wird somit vollkommen durch das Summenzeichen bestimmt. Du musst also eine 0 an der (n+1)-ten Stelle einfügen. Das ist meist einsichtig, weil es auch unserer gewohnten Schreibweise im Dezimalsystem entspricht.
Ist der Wert jedoch negativ, so ist das n-te Bit gleich 1, es geht also mit "negativem Wert" in die Berechnung ein. Nach Definition des Zweierkomplements muss bei einer Ausweitung um 1 Bit aber auch das neue höchstwertige Bit gleich 1 sein. Dieses hat nun aber den Wert 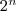 und der ist somit genau doppelt so hoch wie der vorherige. Das muss korrigiert werden. Wie geht das am einfachsten? Beachte, dass das vorherige höchstwertige (n-1)-te Bit nun zum "Summenzeichen gehört". Wenn ich dieses Bit auf 1 lasse, dann wird von und der ist somit genau doppelt so hoch wie der vorherige. Das muss korrigiert werden. Wie geht das am einfachsten? Beachte, dass das vorherige höchstwertige (n-1)-te Bit nun zum "Summenzeichen gehört". Wenn ich dieses Bit auf 1 lasse, dann wird von 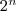 gerade gerade 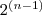 und damit die "überzählige Hälfte" abgezogen. Beispiel: -128 ist 80 hex, nämlich und damit die "überzählige Hälfte" abgezogen. Beispiel: -128 ist 80 hex, nämlich  . Wird das nun auf 9 Bit ausgeweitet, so lautet der Wert 180 hex = . Wird das nun auf 9 Bit ausgeweitet, so lautet der Wert 180 hex = 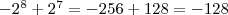 . .
Diese Ausweitung kannst Du nun beliebig fortsetzen, bei 16 Bit wäre das dann FF80 hex (rechne es im Zweifel mal durch).
In der Anwendung ist es ganz einfach: man muss einfach das oberste Bit expandieren. Also FC hex => oberstes Bit = 1, somit 16 Bit = FFFC hex. Oder 47 hex => oberstes Bit 0, somit 0047hex mit 16 Bit. Das ganze nennt man dann anschaulich "Sign Extension". |
|
|
| |
|
|
|
 |
|
|
|
|
 ::
::