| Author |
Message |
rgerhards
|
|
Post subject: Darstellung einer Matrix als Produkt von Elementarmatrizen
 Posted: Oct 18, 2008 - 10:32 AM Posted: Oct 18, 2008 - 10:32 AM
|
|
Joined: Sep 25, 2006
Posts: 688
Status: Offline
|
|
[work in progress]
Eine invertierbare Matrix kann auch als Produkt von Elementarmatrizen dargestellt werden.
Sei 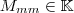 eine beliebige Matrix und sei eine beliebige Matrix und sei 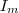 die zugehörige Einheitsmatrix. die zugehörige Einheitsmatrix.
Zunächst ein konkretes Beispiel:
Die Matrix 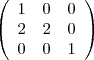 soll als Produkt von Elementarmatrizen dargestellt werden. Dazu ist sie mittels elementarer Zeilenumformungen umzustellen. soll als Produkt von Elementarmatrizen dargestellt werden. Dazu ist sie mittels elementarer Zeilenumformungen umzustellen.
Man beachte, dass bei diesen Zeilenumformungen die Multiplikation mit der Elementarmatrix immer von Links erfolgen muss, d.h. die Elementarmatrix steht links, die aktuell zu betrachtende "Aufgabematrix" rechts. Dies ist wichtig, da die Matrizenmultiplikation nicht kommutativ ist.
1. Umformung, Typ 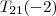
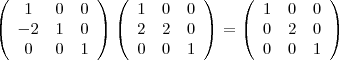
2. Umformung, Typ 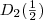
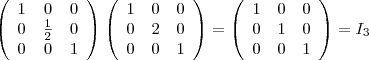
Die Matrix ist nun in Treppennormalform und zeilenäquivalent zur Einheitsmatrix 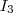 . Sie ist somit invertierbar. . Sie ist somit invertierbar.
Kurz geschrieben, wurden folgende Umformungen durchgeführt:
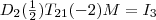
Um die Ausgangsmatrix 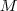 als Produkt von Elementarmatrizen zu bekommen, müssen wir nun die Operationen invertieren. Ich denke, der Weg müsste dieser sein: als Produkt von Elementarmatrizen zu bekommen, müssen wir nun die Operationen invertieren. Ich denke, der Weg müsste dieser sein:
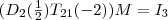
Dies wird nun multipliziert mit 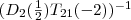 , dem multiplikativen Inversen des Klammerausdrucks. Es ergibt sich damit der folgende Ausdruck: , dem multiplikativen Inversen des Klammerausdrucks. Es ergibt sich damit der folgende Ausdruck:
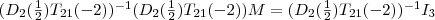
Die Multiplikation einer Elementarmatrix mit ihrer Inversen ergibt aber nun gerade die Einheitsmatrix. Die, multipliziert mir einer beliebigen anderen Matrix, ergibt die andere Matrix. Die Klammerausdrücke vor 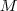 fallen somit weg: fallen somit weg:
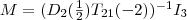
Nun betrachten wir den Klammerterm 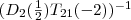 und überführen diesen in eine Form, in der wiederum nur Elementarmatrizen auftreten. Zunächst einmal gilt: und überführen diesen in eine Form, in der wiederum nur Elementarmatrizen auftreten. Zunächst einmal gilt:
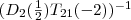
Wegen der Nicht-Kommutativität muss die Reihenfolge vertauscht werden!
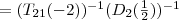
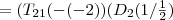
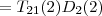
Dies wieder eingesetzt ergibt das gewünschte Produkt der Elementarmatrizen:
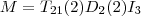
Hinweis: hier bleibt 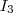 "hinten" stehen, da hier ja nichts mehr invertiert wird, sondern nur eingesetzt. "hinten" stehen, da hier ja nichts mehr invertiert wird, sondern nur eingesetzt.
Und jetzt rechnen wir das wieder exemplarisch:
1. Schritt 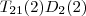
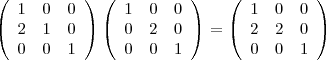
2. Schritt, Zwischenergebnis multipliziert mit 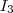
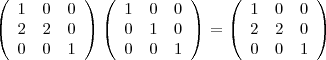
Wie auffällt, ist der zweite Schritt gar nicht mehr nötig.. Dies kommt daher, da 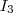 , die Einheitsmatrix, ja das neutrale Element hinsichtlich der Multiplikation ist, und damit gilt , die Einheitsmatrix, ja das neutrale Element hinsichtlich der Multiplikation ist, und damit gilt 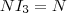 für beliebige Matrizen für beliebige Matrizen 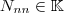 . Das hatten wir uns übrigens oben bei der Multiplikation der Elementarmatrizen mir ihren Inversen schon benutzt. Jetzt können wir unseren Ausdruck natürlich auch noch weiter vereinfachen: . Das hatten wir uns übrigens oben bei der Multiplikation der Elementarmatrizen mir ihren Inversen schon benutzt. Jetzt können wir unseren Ausdruck natürlich auch noch weiter vereinfachen:
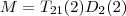
Fazit
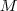 ist also das Produkt des Inversen der Elementarmatrizen, die zu seiner Umformung in die Treppennormalform verwendet werden müssen. ist also das Produkt des Inversen der Elementarmatrizen, die zu seiner Umformung in die Treppennormalform verwendet werden müssen. |
|
|
| |
|
|
|
 |
|
|
|
|
 ::
::