Astronomy and Space Flight, Astronomie und Raumfahrt und dies und das... :: Thema anzeigen - Darstellung einer Matrix als Produkt von Elementarmatrizen

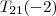
Achtung: Dies ist eine historische Web-Site. Aktuell ist https://rainer.gerhards.net/ (engl) bzw https://www.rainer-gerhards.de/ (deutsch). Alle dynamischen Funktionen, Formulare etc auf dieser Seite sind abgeschaltet.
Datenschutzerklärung Impressum

Astronomy and Space Flight, Astronomie und Raumfahrt und dies und das...

Mathematik - Darstellung einer Matrix als Produkt von Elementarmatrizen

rgerhards - 18.10.2008, 10:32 Uhr
Titel: Darstellung einer Matrix als Produkt von Elementarmatrizen

[work in progress]

Eine invertierbare Matrix kann auch als Produkt von Elementarmatrizen dargestellt werden.

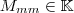Sei $M_{mm} \in \mathbb{K}$ eine beliebige Matrix und sei I_m

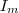die zugehörige Einheitsmatrix.

Zunächst ein konkretes Beispiel:

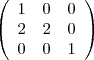Die Matrix $\left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right)$ soll als Produkt von Elementarmatrizen dargestellt werden. Dazu ist sie mittels elementarer Zeilenumformungen umzustellen.

Man beachte, dass bei diesen Zeilenumformungen die Multiplikation mit der Elementarmatrix immer von Links erfolgen muss, d.h. die Elementarmatrix steht links, die aktuell zu betrachtende "Aufgabematrix" rechts. Dies ist wichtig, da die Matrizenmultiplikation nicht kommutativ ist.

1. Umformung, Typ $T_{21}(-2)$

$\left( \begin{array}{ccc} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right)$

2. Umformung, Typ $D_2(\frac{1}{2})$

$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) = I_3$

Die Matrix ist nun in Treppennormalform und zeilenäquivalent zur Einheitsmatrix I_3

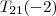
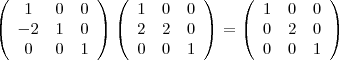
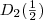
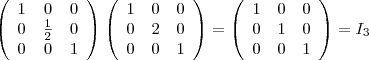
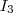. Sie ist somit invertierbar.

Kurz geschrieben, wurden folgende Umformungen durchgeführt:

$D_2(\frac{1}{2})T_{21}(-2)M = I_3$

Um die Ausgangsmatrix

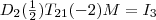
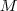als Produkt von Elementarmatrizen zu bekommen, müssen wir nun die Operationen invertieren. Ich denke, der Weg müsste dieser sein:

$(D_2(\frac{1}{2})T_{21}(-2))M = I_3$

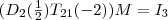
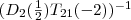Dies wird nun multipliziert mit $(D_2(\frac{1}{2})T_{21}(-2))^{-1}$ , dem multiplikativen Inversen des Klammerausdrucks. Es ergibt sich damit der folgende Ausdruck:

$(D_2(\frac{1}{2})T_{21}(-2))^{-1}(D_2(\frac{1}{2})T_{21}(-2))M = (D_2(\frac{1}{2})T_{21}(-2))^{-1}I_3$

Die Multiplikation einer Elementarmatrix mit ihrer Inversen ergibt aber nun gerade die Einheitsmatrix. Die, multipliziert mir einer beliebigen anderen Matrix, ergibt die andere Matrix. Die Klammerausdrücke vor

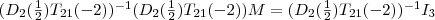
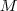fallen somit weg:
$M = (D_2(\frac{1}{2})T_{21}(-2))^{-1}I_3$

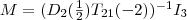
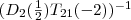Nun betrachten wir den Klammerterm $(D_2(\frac{1}{2})T_{21}(-2))^{-1}$ und überführen diesen in eine Form, in der wiederum nur Elementarmatrizen auftreten. Zunächst einmal gilt:

$(D_2(\frac{1}{2})T_{21}(-2))^{-1}$

Wegen der Nicht-Kommutativität muss die Reihenfolge vertauscht werden!
$= (T_{21}(-2))^{-1}(D_2(\frac{1}{2}))^{-1}$

$= (T_{21}(-(-2))(D_2(1/{\frac{1}{2}})$

$= T_{21}(2)D_2(2)$

Dies wieder eingesetzt ergibt das gewünschte Produkt der Elementarmatrizen:

$M = T_{21}(2)D_2(2)I_3$

Hinweis: hier bleibt I_3

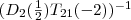
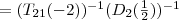
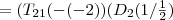
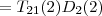
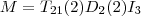
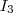"hinten" stehen, da hier ja nichts mehr invertiert wird, sondern nur eingesetzt.

Und jetzt rechnen wir das wieder exemplarisch:

1. Schritt $T_{21}(2)D_2(2)$

$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right)$

2. Schritt, Zwischenergebnis multipliziert mit I_3

$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right)$

Wie auffällt, ist der zweite Schritt gar nicht mehr nötig.. Dies kommt daher, da I_3

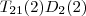
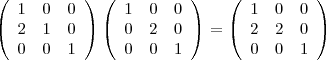
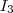
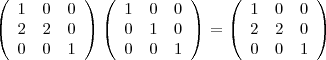
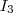, die Einheitsmatrix, ja das neutrale Element hinsichtlich der Multiplikation ist, und damit gilt NI_3= N

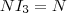für beliebige Matrizen 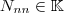$N_{nn} \in \mathbb{K}$ . Das hatten wir uns übrigens oben bei der Multiplikation der Elementarmatrizen mir ihren Inversen schon benutzt. Jetzt können wir unseren Ausdruck natürlich auch noch weiter vereinfachen:

$M = T_{21}(2)D_2(2)$

Fazit

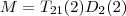
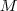ist also das Produkt des Inversen der Elementarmatrizen, die zu seiner Umformung in die Treppennormalform verwendet werden müssen.