| Autor |
Nachricht |
rgerhards
|
|
Titel: Mathematische Darstellung/Rechenanlagen - Ganzzahlen
 Verfasst am: 17.11.2008, 12:59 Uhr Verfasst am: 17.11.2008, 12:59 Uhr
|
|
Anmeldung: 25. Sep 2006
Beiträge: 688
|
|
Ich möchte einmal festhalten, wie Objekte von Rechenanlagen meiner Meinung nach mathematisch definiert sind. Beginnen möchte ich mit den Ganzzahlen.
Sei 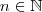 gleich der Wortbreite der Maschine. Seien Ganzzahlen auf der Maschine genau in Wortbreite realisiert. gleich der Wortbreite der Maschine. Seien Ganzzahlen auf der Maschine genau in Wortbreite realisiert.
Sei 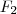 der Körper der Binärzahlen, mit den Symbolen "0" und "1" durch unterschiedliche Spannungspotentiale realisiert. der Körper der Binärzahlen, mit den Symbolen "0" und "1" durch unterschiedliche Spannungspotentiale realisiert.
Dann ist eine vorzeichenlose Ganzzahl ein 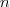 -dimensionaler Vektorraum über -dimensionaler Vektorraum über 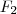 , also , also 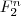 . .
Dann kann eine vorzeichenbehaftete Ganzzahl ebenfalls ein 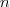 -dimensionaler Vektorraum über -dimensionaler Vektorraum über 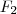 , also , also 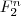 , allerdings mit der Besonderheit, dass die , allerdings mit der Besonderheit, dass die 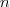 -te Dimension in zwei -te Dimension in zwei 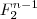 -Unterräume "zerfällt". Dies wäre dann die Darstellung in der Form "Betrag und Vorzeichen". Kennzeichnend ist hier, dass der darstellbare Zahlenraum symmetrisch ist (da ja zwei vollständige Unterräume vorliegen). Allerdings gibt es dann sowohl eine negative und positive 0, da der Nullvektor natürlich in beiden Unterräumen enthalten sein muss. -Unterräume "zerfällt". Dies wäre dann die Darstellung in der Form "Betrag und Vorzeichen". Kennzeichnend ist hier, dass der darstellbare Zahlenraum symmetrisch ist (da ja zwei vollständige Unterräume vorliegen). Allerdings gibt es dann sowohl eine negative und positive 0, da der Nullvektor natürlich in beiden Unterräumen enthalten sein muss.
Zur Vermeidung der negativen 0 findet üblicherweise eine andere Darstellung Anwendung, die des sogenannten Zweierkomplement. Hierbei wird der Nullvektor des die negativen Zahlen abbildenden Unterraumes ersetzt durch den Wert 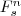 und die restlichen Vektoren werden auch transformiert (und zwar dergestallt, dass immer gilt und die restlichen Vektoren werden auch transformiert (und zwar dergestallt, dass immer gilt 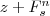 ). ).
Ich stelle mir nun die Frage, ob eine Ziffernfolge in Zweierkomplementdarstellung noch einen Vektorraum bildet. Wird die Struktur des Vektorraumes nicht dadurch zerstört, dass der "negative" Nullvektor nun mit der übergeordneten Dimension des Vorzeichens verschränkt wird und die Transformation der Vektoren in diesem (und nur in diesem) Unterraum statt findet?
Ich gebe gerne zu, dass diese Frage für praktische Belange wahrscheinlich vollkommen irrelevant ist. Für das theoretische Verständnis erscheint mir die Frage allerdings durchaus belangreich. |
|
|
| |
|
|
|
 |
|
|
|
|
 ::
::