| Author |
Message |
rgerhards
|
|
Post subject: 1661 SS EA 1-3 bc)
 Posted: Apr 19, 2009 - 08:41 PM Posted: Apr 19, 2009 - 08:41 PM
|
|
Joined: Sep 25, 2006
Posts: 688
Status: Offline
|
|
Die Kosten werden laut Aufgabenstellung durch den  bestimmt. Es ist also zu ermitteln, wie oft dieser durchlaufen wird. Ist lediglich ein Element vorhanden, so wird er kein Mal durchlaufen, da die Rekursion unmittelbar mit dem allerersten bestimmt. Es ist also zu ermitteln, wie oft dieser durchlaufen wird. Ist lediglich ein Element vorhanden, so wird er kein Mal durchlaufen, da die Rekursion unmittelbar mit dem allerersten 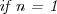 terminiert. Ist terminiert. Ist 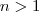 , so werden jeweils die zwei Teile des Arrays durchlaufen. Laut Augabe handelt es sich bei , so werden jeweils die zwei Teile des Arrays durchlaufen. Laut Augabe handelt es sich bei 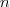 um eine Zweierpotenz, so dass immer zwei Teilarrays existieren. In jedem Durchlauf ist dabei eine Ausführung des um eine Zweierpotenz, so dass immer zwei Teilarrays existieren. In jedem Durchlauf ist dabei eine Ausführung des  erforderlich, sowie zusätzlich die Anzahl der Ausführungen aller weiteren Rekursionsstufen (also erforderlich, sowie zusätzlich die Anzahl der Ausführungen aller weiteren Rekursionsstufen (also 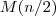 ). Da beide Teilarrays durchlaufen werden, muss diese Laufzeit doppelt in die ). Da beide Teilarrays durchlaufen werden, muss diese Laufzeit doppelt in die
Betrachtung einfliessen. Die Funktion 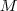 hat damit folgende Struktur: hat damit folgende Struktur:
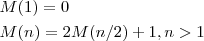
Teil c
Da es sich bei $n$ laut Vorgabe um eine Zweierpotenz handelt, ist
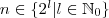
Somit gibt es stets ein 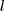 für das gilt für das gilt 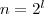 . .
Einsetzen in die Rekursion liefert (redundante Klammern zur Verdeutlichung):
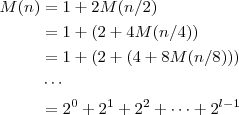
Dies entspricht aber gerade der geschlossenen Formel

Ich führe den Beweis mittels vollständiger Induktion über 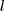 . .
Für 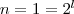 ist ist  . .
Im Induktionsanfang gilt somit
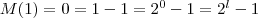
womit der Induktionsanfang bewiesen ist.
In der Induktionsannahme nehmen wir an, dass für ein 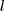 gilt gilt
 . .
Dann gilt für  : :
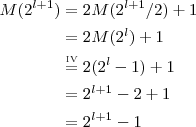
Mit dem Prinzip der vollständigen Induktion folgt somit die Behauptung. |
|
|
| |
|
|
|
 |
|
|
|
|
 ::
::