| Author |
Message |
rgerhards
|
|
Post subject: An einer Komposition beteiligte Mengen
 Posted: Oct 15, 2008 - 01:30 PM Posted: Oct 15, 2008 - 01:30 PM
|
|
Joined: Sep 25, 2006
Posts: 688
Status: Offline
|
|
Eine Komposition ist nichts anderes als eine eigene Abbildung, deren Rechenvorschrift nun "zufälligerweise" die Komposition von zwei anderen Abbildungen ist. Also so etwas:
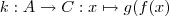
Das ist übrigens überhaupt nichts besonders. Ein Beispiel:
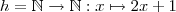
ist ja nichts anderes als
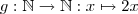

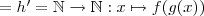
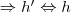
Die Komposition von Abbildungen ist also der absolute Normalfall, nur sehen wir das meist nicht bewusst.
Nun zur Betrachtung der beteiligten Mengen. Es sei:
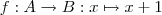
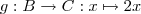
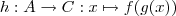
A und B sind die Definitions- und Zielmenge der Funktion. Betrachten wir nun die Menge B, quasi die "Zwischenmenge". Die kann unter Umständen sehr "unhandlich" zu notieren sein, so dass man sie nicht mehr einfach benennen kann. Das ist übrigens analog dazu zu sehen, dass ja auch die Bildmenge "sehr unhandlich" zu notieren ist. Bei der Bildmenge hat man daher die Zielmenge als Generalisierung eingeführt, nämlich die Menge, die eine einfach zu notierenden Obermenge der Bildmenge ist.
So etwas gibt es bei der Definitionsmenge nicht - oder etwa doch? Ich habe in einigen Quellen (darunter auch Wikipedia[1]) den Begriff der Quellmenge gefunden. Auch diese ist eine Obermenge der Urbildmenge, analog zu Bild-/Definitionsmenge zu verstehen. Mit Hilfe der Quellmenge kann ich nun wieder kompakt notieren, welche Werte ein Abbildung potentiell abbilden kann. Dies ist zu unterscheiden von den Werten, die sie aktuell, im konkreten Fall, auch tatsächlich abbildet.
Die "Zwischenmenge B" der Komposition ist nun eine Obermenge sowohl der Zielmenge von g als auch der Quellmenge von f. Dies ist notwendig, damit g nur Bilder erzeugt, die f auch potentiell abbilden kann. Aus Gründen der Übersichtlichkeit und leichten Handhabbarkeit wird die Menge der aktuell abgebildeten Elemente demgegenüber nicht spezifiziert.
Und jetzt kommt die ganz dicke Warnung: das ist mein Verständnis der Sachlage. Ich bin mir zwar mittlerweile ziemlich sicher, dass es so ist. Da es sich dann aber nur um Notationskonventionen handelt, kann ich es nicht wirklich beweisen. Eine sonstige starke Bestätigung dieser Sichtweise steht noch aus. Was ich sage kann also auch gänzlich falsch sein! (Darum würde ich mich auch über Feedback sehr freuen).
[1] http://de.wikipedia.org/wiki/Funktion_(Mathematik) |
|
|
| |
|
|
|
 |
|
|
|
|
 ::
::