Achtung: Dies ist eine historische Web-Site.
Aktuell ist https://rainer.gerhards.net/ (engl) bzw
https://www.rainer-gerhards.de/ (deutsch).
Alle dynamischen Funktionen, Formulare etc auf dieser Seite sind abgeschaltet.
Datenschutzerklärung
Impressum
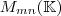 aber als spezielle Schreibweise eines Vektors
aber als spezielle Schreibweise eines Vektors 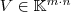 betrachten. Jede Matrix kann dann in einen Vektor überführt werden und jeder Vektor mit
betrachten. Jede Matrix kann dann in einen Vektor überführt werden und jeder Vektor mit  Komponenten in eine Matrix. Insbesondere gibt es somit verschiedene Schreibweisen des selben mathematischen Objekts, eben
Komponenten in eine Matrix. Insbesondere gibt es somit verschiedene Schreibweisen des selben mathematischen Objekts, eben 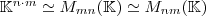 sowie potentiell noch einige andere Matrizen, nämlich denen, deren Produkt der Zeilen- und Spaltenanzahl gleich
sowie potentiell noch einige andere Matrizen, nämlich denen, deren Produkt der Zeilen- und Spaltenanzahl gleich  ist. Generell lässt sich damit sagen
ist. Generell lässt sich damit sagen
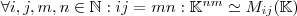
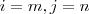 und hierfür die Transformationsfunktion angeben. Bei der Transformation handelt es sich um eine lineare Abbildung. Sei
und hierfür die Transformationsfunktion angeben. Bei der Transformation handelt es sich um eine lineare Abbildung. Sei 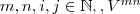 ein
ein  -dimensionaler Vektorraum über einem Körper
-dimensionaler Vektorraum über einem Körper 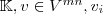 das Element in der
das Element in der  -ten Zeile von
-ten Zeile von 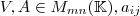 das Element von
das Element von 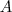 in der
in der  -ten Zeile und
-ten Zeile und 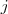 -ten Spalte. Dann ist
-ten Spalte. Dann ist
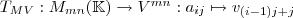
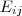 die Elementarmatrix mit einer 1 an der Position
die Elementarmatrix mit einer 1 an der Position 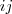 und ansonsten nur Nullen. Sei
und ansonsten nur Nullen. Sei 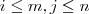 , dann kann mit ihrer Hilfe ein Basisvektor die Basis einer Dimension aus der Matrix
, dann kann mit ihrer Hilfe ein Basisvektor die Basis einer Dimension aus der Matrix 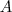 "extrahiert" werden, und zwar in der folgenden Weise:
"extrahiert" werden, und zwar in der folgenden Weise:
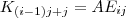
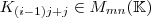 die "Koordinatenmatrix" (mir ist kein besserer Name eingefallen), die genau eine Koordinate der ursprünglichen Matrix beeinhaltet und ansonsten nur Nullen. Dies Umformung wird für alle i, j durchgeführt. Im Ergebnis erhalte ich eine Menge
die "Koordinatenmatrix" (mir ist kein besserer Name eingefallen), die genau eine Koordinate der ursprünglichen Matrix beeinhaltet und ansonsten nur Nullen. Dies Umformung wird für alle i, j durchgeführt. Im Ergebnis erhalte ich eine Menge 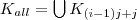 der Mächtigkeit
der Mächtigkeit 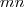 .
.
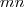 -Tupel des Vektors zu bilden. Wenn ich eine Ordnungsrelation über dieser Menge definiere, so dass die Elemetne aufsteigend nach
-Tupel des Vektors zu bilden. Wenn ich eine Ordnungsrelation über dieser Menge definiere, so dass die Elemetne aufsteigend nach 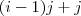 geordnet sind, so habe ich auch schon das Tupel und in zwar in der richtigen Reihenfolge. Die Komponenten haben aber noch die falsche Struktur. Die einzelnen Komponenten, die Koordinaten, liegen nämlich noch in Matrixform vor. Durch Zeilen- und Spaltenumformungen kann ich das nun beheben, und die Komponente mit der eigentlichen Koordinate aus jeder Matrix extrahieren. Ich transformiere somit jede Matrix
geordnet sind, so habe ich auch schon das Tupel und in zwar in der richtigen Reihenfolge. Die Komponenten haben aber noch die falsche Struktur. Die einzelnen Komponenten, die Koordinaten, liegen nämlich noch in Matrixform vor. Durch Zeilen- und Spaltenumformungen kann ich das nun beheben, und die Komponente mit der eigentlichen Koordinate aus jeder Matrix extrahieren. Ich transformiere somit jede Matrix 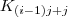 in eine Matrix
in eine Matrix 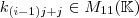 . Die Ränge beider Matrizen sind identisch, damit ist die entsprechenden lineare Abbildung injektiv und damit ist sie bijektiv.
. Die Ränge beider Matrizen sind identisch, damit ist die entsprechenden lineare Abbildung injektiv und damit ist sie bijektiv.
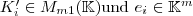 der Einheitsvektor, der in der
der Einheitsvektor, der in der  -ten Komponente eine 1 hat und in allen anderen eine 0. Die Abbildung wird nun folgendermassen vorgenommen:
-ten Komponente eine 1 hat und in allen anderen eine 0. Die Abbildung wird nun folgendermassen vorgenommen:
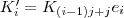
 -ten Spalte extrahieren. Dies geschieht über folgende lineare Abbildung:
-ten Spalte extrahieren. Dies geschieht über folgende lineare Abbildung:
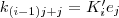
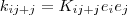 zu schreiben. Dies ist aber nicht möglich, da die Ausgangsmatrix nicht quadratisch sein muss und somit
zu schreiben. Dies ist aber nicht möglich, da die Ausgangsmatrix nicht quadratisch sein muss und somit 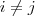 möglich ist. Dann aber verfügen die Einheitsvektoren über unterschiedliche Komponentenanzahl und die Matrizenmltiplikation ist nicht mehr in allen Fällen definiert (stimmt das denn überhaupt...? - nochmal nachdenken).
möglich ist. Dann aber verfügen die Einheitsvektoren über unterschiedliche Komponentenanzahl und die Matrizenmltiplikation ist nicht mehr in allen Fällen definiert (stimmt das denn überhaupt...? - nochmal nachdenken).
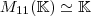 folgt, dass das Koordinatentupel nun ein Vektor
folgt, dass das Koordinatentupel nun ein Vektor 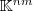 ist. Das Tupel ist somit das gesuchte Bild
ist. Das Tupel ist somit das gesuchte Bild 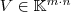 der Matrix
der Matrix 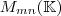 .
.