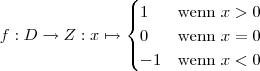Gerhards.net verwendet Cookies um die Nutzung der Seite zu erleichtern. Mit der weiteren Nutzung dieser Seite erklären Sie sich mit der Verwendung von Cookies einverstanden. In unserer Datenschutzerklärung erfahren Sie weitere Informationen.OkRead more
Astronomy and Space Flight, Astronomie und Raumfahrt und dies und das...
Mathematik - "Fallunterscheidungen" in Funktionen
rgerhards - 15.10.2008, 12:58 Uhr
Titel: "Fallunterscheidungen" in Funktionen
Ähnlich der Programmierung gibt es auch in der Mathematik "Fallunterscheidungen". Ich bin mir nicht sicher, ob diese Bezeichnung korrekt ist (Hinweise willkommen!), aber die Funktion ist jedenfalls die Gleiche.
Üblicherweise betrachten wir Funktionen (D und Z sind die Definitions- und Zielmenge):
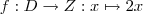
Hier ist die Rechenvorschrift 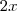 für alle
für alle  die gleiche. Damit lassen sich aber nicht alle möglichen Funktionen abbilden. Als Beispiel sei der Betrag/Absolutwert genannt. Das Ergebnis von
die gleiche. Damit lassen sich aber nicht alle möglichen Funktionen abbilden. Als Beispiel sei der Betrag/Absolutwert genannt. Das Ergebnis von 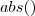 ist dabei für positive Werte exakt der "eingegebene" Wert, für negative x hingegen -x, also der gleiche Wert, jedoch mit positivem Vorzeichen.
ist dabei für positive Werte exakt der "eingegebene" Wert, für negative x hingegen -x, also der gleiche Wert, jedoch mit positivem Vorzeichen.
Ohne eine Unterscheidung der Fälle lässt sich das nun nicht beschreiben. Konkret definiert wird die Funktion dann so:
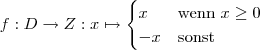
Dabei gibt es natürlich gewisse Freiräume, so hätte ich z. B. anstelle von "sonst" auch 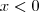 schreiben können.
schreiben können.
Es sind nicht nur 2 Fälle möglich, sondern prinzipiell unendlich viele. Diese werden dann einfach in verschiedene Zeilen geschrieben. Dazu ein Beispiel mit drei Fällen: die Funktion 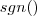 hat den Wert 1, wenn ihr Argument positiv ist, 0, wenn es gleich 0 ist und -1, wenn es negativ ist. Dies kann man so ausdrücken:
hat den Wert 1, wenn ihr Argument positiv ist, 0, wenn es gleich 0 ist und -1, wenn es negativ ist. Dies kann man so ausdrücken:
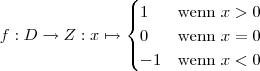
Um mit einer solchen Funktion "rechnen" zu können, muss man auch für jeden Fall getrennte Rechungen anstellen.
In LaTex wird eine solche Formel übrigens solchermassen erstellt:
Code:
f : D \rightarrow Z : x \mapsto
\begin{cases}
1 & \text{wenn } x > 0 \\
0 & \text{wenn } x = 0 \\
-1 & \text{wenn } x < 0 \\
\end{cases}
Alle Zeiten sind GMT + 1 Stunde
PNphpBB2 © 2003-2007
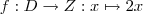
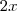 für alle
für alle  die gleiche. Damit lassen sich aber nicht alle möglichen Funktionen abbilden. Als Beispiel sei der Betrag/Absolutwert genannt. Das Ergebnis von
die gleiche. Damit lassen sich aber nicht alle möglichen Funktionen abbilden. Als Beispiel sei der Betrag/Absolutwert genannt. Das Ergebnis von 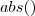 ist dabei für positive Werte exakt der "eingegebene" Wert, für negative x hingegen -x, also der gleiche Wert, jedoch mit positivem Vorzeichen.
ist dabei für positive Werte exakt der "eingegebene" Wert, für negative x hingegen -x, also der gleiche Wert, jedoch mit positivem Vorzeichen.
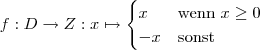
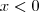 schreiben können.
schreiben können.
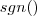 hat den Wert 1, wenn ihr Argument positiv ist, 0, wenn es gleich 0 ist und -1, wenn es negativ ist. Dies kann man so ausdrücken:
hat den Wert 1, wenn ihr Argument positiv ist, 0, wenn es gleich 0 ist und -1, wenn es negativ ist. Dies kann man so ausdrücken: